
Lesson Concept: Math Challenge with Sol Le Witt
Students explore conceptual art by Sol LeWitt to expand their understanding of geometric concepts, creatively play with mathematical ideas, and become inspired to make art of their own.
Conceptual Art
“What the work looks like isn’t too important…No matter what form it may finally have, it must begin with an idea.” — Sol LeWitt
In the VMFA’s Lewis Contemporary Galleries, visitors are able to experience Sol LeWitt’s ideas at work in a structure that is at once simple and complex. Titled 1 2 3 4 5 6, and made of painted wood in 1978, it is part of a series of modular cubic structures the artist began in the mid-1960s.
A founder of Conceptual Art, a movement that emphasized a rational, objective approach to form, LeWitt sought to make work that stimulates the mind of the spectator. In his 1967 essay Paragraphs on Conceptual Art, LeWitt maintained that the idea behind any particular work of art need not be complex, and that “the mathematics used by most artists is simple arithmetic or simple number systems.” Indeed this intricate tower comes from a simple routine for multiplication—1×1, 2×2, 3×3, etc.— that results in adding one more row to each descending level of stacked cubes. The top tier is a single unit, while the bottom tier is cubed 6x6x6 units. This basic formula yields surprisingly complex visual results as the viewer peers into the work from various angles.
Taking a Closer Look in the Gallery
LeWitt also recognized and valued the perception of the spectator in the success of the artwork. Speaking of the artist’s role, he noted, “Once it is out of his hand, the artist has no control over how the viewer will perceive the work. Different people will understand the same thing in a different way.” Taking this to heart, we are invited as viewers to experience 1 2 3 4 5 6 in the gallery space and uncover our own ideas and understanding about space, form, scale, similarity, and more.
Let’s accept that invitation to play around with some geometric ideas your students may be exploring. Click on the image to open a new tab and enter the VMFA’s Lewis Contemporary Galleries with Google’s Museum View.
Drawing Challenge
True to LeWitt’s intention, visitors to VMFA’s galleries understand 1 2 3 4 5 6 in different ways. Close examination of the structure can help students begin to grapple with their own ideas about this artwork. To help spur their examination, encourage computational thinking, and prompt a rich discussion about the mathematics at work in this piece, offer them this open-ended challenge:
“Make a drawing of this artwork that includes as much information about the piece as possible. See how much information you can capture in ten minutes.” (timing restriction optional)
There is no correct way to accomplish the task. Some students may wish to think of their drawing as a diagram. Others may attempt to draw a portrait of the structure, seeking to capture every nuance. Perhaps others will focus on only one aspect of the work such as a corner, a single cube, or the outline of the structure. Any way the student wishes to approach the task is fine.
Come back as a group and share observations.
- Did they make any discoveries about the structure that they had not initially noticed?
- What was difficult or easy about making the sketch?
- Looking at this challenge through a mathematical lens what ideas did they uncover?
Make a list of student observations that address Geometry concepts they may be currently examining in the classroom.
Taking a Closer Look: Proportions
In a 1974 interview, Sol LeWitt described an organizing principle for his modular cube series. He decided that the proportion of enclosed space to the material used to build would be 8.5:1. Speaking of a structure in his studio he noted, “You get the wood, which is, in this case, a half-inch square. So that decides the form.”
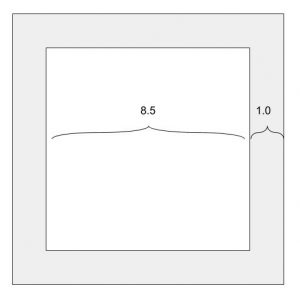
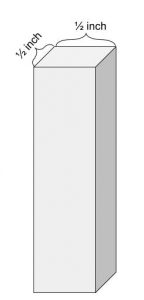
The wood used to make 1 2 3 4 5 6 is also a 1/2″ x 1/2″ dowel.
Knowing LeWitt’s proportional system, we can calculate the size of the modular cubes used in the work and even the measurement of the base (29″ x 29″). Challenge students to write an equation demonstrating this.
The Tinkercad model below uses the 8.5:1 ratio:
Tinkercad Challenge
Tinkercad is an online tool students can use to design 3-D models. Below is a rendition of Sol LeWitt’s 1 2 3 4 5 6 using Tinkercad software. Challenge students to use Tinkercad to create their own structure using LeWitt’s approach to art-making as inspiration. Using the list of concepts generated though the Drawing Challenge, ask them to determine a mathematical concept to be the IDEA behind the artwork. What FORM will this idea take? Students should make notations and sketch out plans on paper, as Sol LeWitt did, before beginning to tinker.
Sources
LeWitt, Sol. “Paragraphs on Conceptual Art.” Artforum 5, no. 10 (June 1967): 79-83.
LeWitt, Sol, Nicholas Baume, and Jonathan Flatley. Sol Lewitt: Structures, 1965-2006. New York: Public Art Fund, 2011.
LeWitt, Sol, Dean Swanson, and Martin Friedman. Lewitt X 2: Sol Lewitt: Structure and Line: Selections from the Lewitt Collection: Madison: Madison Museum of Contemporary Art, 2006.
“Oral History Interview with Sol LeWitt, 1974 July 15.” Interview by Paul Cummings. Archives of American Art. Accessed July 05, 2018. https://www.aaa.si.edu/collections/interviews/oral-history-interview-sol-lewitt-12701#transcript.
Ravenal, John B. Modern and Contemporary Art of the Virginia Museum of Fine Arts. Richmond: Virginia Museum of Fine Arts, 2007. (Pp. 140-141).
Standards of Learning
Mathematics: 6.4, 6.6, 6.7.c, 6.12, 7.3 7.4, 7.6, 8.6, 8.8, G.13, G.14
Visual Arts: 6.1, 6.5, 6.14, 6.19, 7.1, 7.3, 7.4, 7.6, 7.17, 7.18, 8.1, 8.4, 8.8, 8.11, 8.15, 8.21, AI.2, AI.8, AI.13, AI.17, AI.20, AII.2, AII.5, AII.19, AII.24

